coder . cl

If you have pretty clear programming concepts, learning new programming languages is not so hard as it seems. But those concepts are hard to understand. I will use my most recent learnt programming language, where probably you already know about what is it. Haskell is a programming language fulfilled with concepts, mostly based on mathematical abstractions inherited from Lambda Calculus, Combinatory Logic and Category Theory, among other topics that are covering its well known constructs, like Monads — which is inherited from Category Theory. You can understand how to work with Monads, like the IO Monad, StateMonad, and similar ones, but you need to understand the Monad basis from the perspective of the Category Theory to build your own Monads as abstractions. I am pretty sure that you can find theoretical basis on most programming abstractions, once you understand those theoretical basis, you are able to build well structured abstractions by yourself. Even if your knowledge on each topic is not so deep an abstraction variant, you can understand those concepts behind each construct and implement not so formal variants of each abstraction.

I will use the classic discussion about the Monadic perspective of jQuery. Along Monad implementations, you have a natural transformation from a type B to a composite type A B, to build chained or sequenced computations with identity. But the sequence or computation chain type is preserved along the process, as it is required from its formal definition. On jQuery you lost that composite type, falling in different composite types along the computation chain.

$('#select-node-id').
    find('element').
    each(function (idx, elm) {
        $(elm).attr('id', 'seq' + idx);
    }).
    addClass('list-nodes').
    find('element:first').
    addClass('first');

If you have a look on the code snippet above, you have a computation chain, where the composite type can vary between Node String, NodeList String and DOMString String. In other words those types are three different composite types A B, A C and A D. The type sequence can be enumerated as follows.

1. Node DOMString
2. NodeList DOMString
3. NodeList DOMString
4. Node DOMString
5. NodeList DOMString
6. Node DOMString
7. Node DOMString
8. Node DOMString

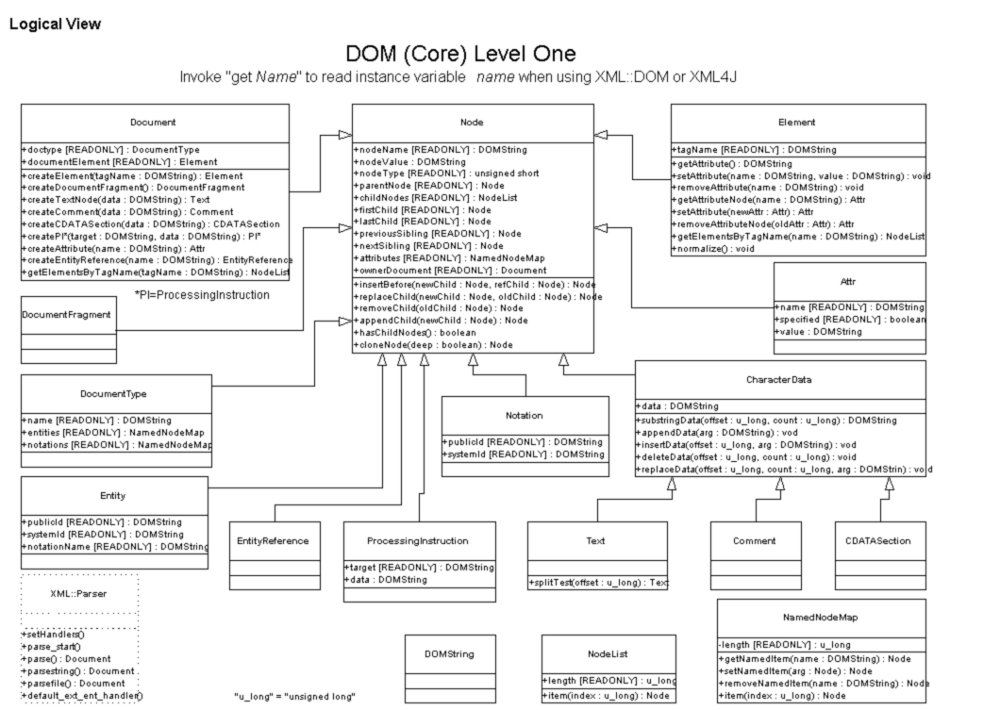
If the chain or sequence is loosing its type, which its identity should be bound to that type, jQuery is not a Monad. Please have a look on the Document Object Model (DOM) class diagram bellow. So, each type on the sequence have an unbound type, and the last selected node in the sequence have a different type, where the last Monad have a different composite type from the original requested composite type. This breaks the identity Monadic law, as does every change on the composite type along the sequence.

Document Object Model Class Diagram

A Haskellish solution is to create a second composite type as follows.

data NodeSelector = NodeSelector DOMString deriving (Eq, Show)


data NodeUntyped = Node NodeSelector
                   | NodeList NodeSelector
                   | DOMString NodeSelector
                   deriving (Eq, Show)


newtype NodesM n = NodesM n { toNode :: n }


instance Monad NodesM where
  return = NodesM
  f >>= g = g $ toNode f

Where each operation — to make it Monadic — should be implemented over NodesM NodeUntyped, without variants on the bound type as meeting the identity and transformation Monadic laws. This will preserve the required set of Categories that meets the original model. If you do not have a clear concepts about a language, you cannot understand the language itself.